Questão Cespe dificílima saindo do forno no Questão Smart!
Questão do dia:
De uma urna que continha 20 bolas idênticas, identificadas por números de 1 a 20, foi extraída aleatoriamente uma bola. Esse evento define o espaço amostral Ω = {1, 2, 3, ..., 20}.
Considere os seguintes eventos:
A = {a bola retirada da urna é identificada por um número múltiplo de 4};
B = {a bola retirada da urna é identificada por um número múltiplo de 5}.
A partir das probabilidades P(A), P(B) e P(A∪B) — que são, respectivamente, as probabilidades de os eventos A, B e A∪B ocorrerem —, considere o argumento formado pelas premissas P1 e P2 e pela conclusão C, em que
P1: Se P(A) = ¼ e P(B) = 1/5, então P(AUB) = 9/20
P2: P (AUB) ≠ 9/20
C: P(A) ≠ 1/4 ou P(B) ≠ 1/5
Com base nessas informações, assinale a opção correta.
a) A premissa P1 é uma proposição verdadeira, e a conclusão C é uma proposição falsa.
b) A premissa P2 e a conclusão C são proposições verdadeiras.
c) A conclusão C é falsa, mas o argumento é válido.
d) A premissa P1 é falsa e o argumento não é válido.
e) A premissa P1 e a conclusão C são proposições verdadeiras e o argumento é válido.
Confira a resolução no link
https://youtu.be/T1_Yu3sEbRM
segunda-feira, 11 de junho de 2018
segunda-feira, 21 de maio de 2018
Questão de logaritmos
Bom dia galera! Vamos iniciar a semana com uma questão de logaritmos?
Questão bem tranquila se lembrarmos das propriedades dos logaritmos. Primeiramente vamos montar a equação:
log(a)+log(b)= x
log(250)+log(40)= x
Agora precisamos lembrar que ao somarmos logaritmos de mesma base, podemos manter a base e multiplicar os logaritmandos:
log(250)+log(40)= x
log (250.40)= x
Então temos:
log (10000) = x
Quando a base do logaritmo é oculta, consideramos na base 10. Então transformando em potência:
Igualando as bases
Cortando as bases temos:
x=4
Ou seja, o valor de x é 4, que é o resultado da operação. Gabarito letra D.
Questão bem tranquila se lembrarmos das propriedades dos logaritmos. Primeiramente vamos montar a equação:
log(a)+log(b)= x
log(250)+log(40)= x
Agora precisamos lembrar que ao somarmos logaritmos de mesma base, podemos manter a base e multiplicar os logaritmandos:
log(250)+log(40)= x
log (250.40)= x
Então temos:
log (10000) = x
Quando a base do logaritmo é oculta, consideramos na base 10. Então transformando em potência:
10x=10000
Igualando as bases
10x=104
Cortando as bases temos:
x=4
Ou seja, o valor de x é 4, que é o resultado da operação. Gabarito letra D.
sexta-feira, 18 de maio de 2018
Análise combinatória, anagramas (Funrio)
Questão de anagramas saindo do forno galera!
Um anagrama de uma palavra é uma reordenação qualquer de suas letras. Por exemplo, ATAM e AAMT são anagramas da palavra MATA. O número de anagramas da palavra PORTO é igual a:
a) 60.
b) 76.
c) 90.
d) 112.
e) 120
Confiram a resolução no vídeo:
https://youtu.be/C6RMowMgeq4
terça-feira, 15 de maio de 2018
Razões inversamente proporcionais (FCC)
Mais uma questão resolvida no Clube de Questões - Questões de Concursos Públicos
Questão do dia
Para executar a tarefa de manutenção de 111 microcomputadores, três técnicos judiciários dividiram o total de microcomputadores entre si, na razão inversa de suas respectivas idades: 24, 30 e 36 anos. Assim sendo, o técnico de 30 anos recebeu
(A) 2 micros a mais do que o de 24 anos.
(B) 4 micros a menos do que o de 36 anos.
(C) 4 micros a menos do que o de 24 anos.
(D) 6 micros a menos do que o de 36 anos.
(E) 9 micros a menos do que o de 24 anos.
Confira a resolução no link
https://www.youtube.com/watch?v=kHApcjvzv9Q
terça-feira, 1 de maio de 2018
Questão de geometria plana (Cesgranrio 2018)
Mais uma Questão Smart saindo do forno! A questão é sobre Geometria plana. Confira:
Na Figura a seguir, ABCD é um quadrado de lado 10, e EF é traçado perpendicularmente aos lados AB e CD de modo que a área do triângulo AEF é 30% da área do quadrado.
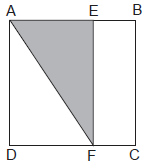
Quanto mede FC?
a) 3
b) 4
c) 5
d) 6
e) 7
https://youtu.be/M3Slk6m1X5E
Na Figura a seguir, ABCD é um quadrado de lado 10, e EF é traçado perpendicularmente aos lados AB e CD de modo que a área do triângulo AEF é 30% da área do quadrado.

Quanto mede FC?
a) 3
b) 4
c) 5
d) 6
e) 7
https://youtu.be/M3Slk6m1X5E
quarta-feira, 25 de abril de 2018
Questão de argumentações lógicas (cespe 2018)
Argumentação lógica é um tópico que vem sido cada vez mais cobrado em provas de raciocínio lógico, principalmente da banca CESPE. Por isso, trouxemos no Questão Smart dessa semana, uma questão de argumentação lógica, confira:
Questão do dia:
As seguintes proposições lógicas formam um conjunto de premissas de um argumento:
• Se Pedro não é músico, então André é servidor da ABIN.
• Se André é servidor da ABIN, então Carlos não é um espião.
• Carlos é um espião.
A partir dessas premissas, julgue o item a seguir, acerca de lógica de argumentação.
Se a proposição lógica “Pedro é músico.” for a conclusão desse argumento, então, as premissas juntamente com essa conclusão constituem um argumento válido.
( )Certo ( ) Errado
Resolução:
https://youtu.be/m4-iwFc3xQQ
Questão do dia:
Ano: 2018
Banca: CESPE
Órgão: ABIN
Prova: Agente de Inteligência
Assunto: proposições lógicas
As seguintes proposições lógicas formam um conjunto de premissas de um argumento:
• Se Pedro não é músico, então André é servidor da ABIN.
• Se André é servidor da ABIN, então Carlos não é um espião.
• Carlos é um espião.
A partir dessas premissas, julgue o item a seguir, acerca de lógica de argumentação.
Se a proposição lógica “Pedro é músico.” for a conclusão desse argumento, então, as premissas juntamente com essa conclusão constituem um argumento válido.
( )Certo ( ) Errado
Resolução:
https://youtu.be/m4-iwFc3xQQ
segunda-feira, 23 de abril de 2018
Questão de proposições lógicas
E aí galera, vamos fazer começar a semana com uma questão de proposições lógicas??
Resolução
Questão interessante de proposições lógicas compostas. A questão informou duas premissas, então precisamos considerar o valor de ambas como verdadeiros, então vamos analisar cada uma.
"Ana é organizada e linda, ou Ana é delicada".
Percebemos que possuímos duas proposições simples ligadas pelo conectivo disjunção (ou)
p1 = Ana é organizada e linda.
p2 = Ana é delicada.
"Ana não é delicada"
Nesse caso, possuímos apenas uma proposição simples, que é a negação da proposição simples P2.
~p2 = Ana não é delicada.
Por ser uma proposição simples, sabemos que ela sozinha é verdadeira. Se ~p2 é verdadeira, então p2 é falsa. Aplicando na nossa primeira premissa:
*para facilitar o entendimento, as proposições verdadeiras serão pintadas de verde e as falsas de vermelha.
Para uma disjunção ser verdadeira, pelo uma das proposições simples precisa ser verdadeira, então a P1 com certeza é verdadeira.
Sabendo que p1 é V e p2 é F, vamos analisar as alternativas:
a) é organizada ou linda.
Alternativa incorreta, Na verdade, Ana é organizada E linda.
b) é organizada e linda.
Alternativa correta, é o que afirma a p1 e sabemos que p1 é verdadeira.
c) é organizada e não é linda
Alternativa incorreta, Na verdade, Ana é organizada elinda.
d) não é organizada e não é linda.
Alternativa incorreta, Na verdade, Ana é organizada e linda.
e) não é organizada e é linda.
Alternativa incorreta, Na verdade, Ana é organizada e linda.
Portanto, gabarito letra B.
Resolução
Questão interessante de proposições lógicas compostas. A questão informou duas premissas, então precisamos considerar o valor de ambas como verdadeiros, então vamos analisar cada uma.
"Ana é organizada e linda, ou Ana é delicada".
Percebemos que possuímos duas proposições simples ligadas pelo conectivo disjunção (ou)
p1 = Ana é organizada e linda.
p2 = Ana é delicada.
"Ana não é delicada"
Nesse caso, possuímos apenas uma proposição simples, que é a negação da proposição simples P2.
~p2 = Ana não é delicada.
Por ser uma proposição simples, sabemos que ela sozinha é verdadeira. Se ~p2 é verdadeira, então p2 é falsa. Aplicando na nossa primeira premissa:
"Ana
é organizada e linda, ou Ana é delicada (F)".
*para facilitar o entendimento, as proposições verdadeiras serão pintadas de verde e as falsas de vermelha.
Para uma disjunção ser verdadeira, pelo uma das proposições simples precisa ser verdadeira, então a P1 com certeza é verdadeira.
"Ana
é organizada e linda (V), ou Ana
é delicada (F)".
Sabendo que p1 é V e p2 é F, vamos analisar as alternativas:
a) é organizada ou linda.
Alternativa incorreta, Na verdade, Ana é organizada E linda.
b) é organizada e linda.
Alternativa correta, é o que afirma a p1 e sabemos que p1 é verdadeira.
c) é organizada e não é linda
Alternativa incorreta, Na verdade, Ana é organizada elinda.
d) não é organizada e não é linda.
Alternativa incorreta, Na verdade, Ana é organizada e linda.
e) não é organizada e é linda.
Alternativa incorreta, Na verdade, Ana é organizada e linda.
Portanto, gabarito letra B.
quinta-feira, 19 de abril de 2018
Questão de condições necessárias e suficientes
Bom dia galera! Um assunto pouco compreendido de RLM é o de condições necessárias e suficientes, por isso trouxe uma questão com a resolução comentada por mim:
Renato ir ao trabalho é condição necessária para André sair de casa, e é condição suficiente para Natália ir ao cinema. Por outro lado, Marcos encontrar Camila é condição necessária e suficiente para José ficar alegre e é condição necessária para Natália ir ao cinema. José não ficou alegre.
Logo:
a) Renato não foi ao trabalho e Marcos não encontrou Camila.
b) Natália foi ao cinema ou Marcos encontrou Camila.
c) Se o André não saiu de casa, então, Marcos encontrou Camila.
d) André saiu de casa e Renato não foi ao trabalho.
Resposta:
Renato ir ao trabalho é condição necessária para André sair de casa, e é condição suficiente para Natália ir ao cinema. Por outro lado, Marcos encontrar Camila é condição necessária e suficiente para José ficar alegre e é condição necessária para Natália ir ao cinema. José não ficou alegre.
Logo:
a) Renato não foi ao trabalho e Marcos não encontrou Camila.
b) Natália foi ao cinema ou Marcos encontrou Camila.
c) Se o André não saiu de casa, então, Marcos encontrou Camila.
d) André saiu de casa e Renato não foi ao trabalho.
Resposta:
Sabemos que as
condições necessárias e suficientes são aplicadas às proposições
condicionais e bicondicionais. De forma resumida, podemos que dizer
que:
Em uma proposição
condicional verdadeira, a primeira é suficiente para a segunda e a
segunda é necessária para a primeira.
Em uma proposição
bicondicional verdadeira, ambas são suficientes e necessárias uma à
outra.
Então vamos
analisar cada informação e montar nossas proposições:
Renato ir ao
trabalho é condição necessária para André sair de casa.
Aplicando a regra da
condição necessária, sabemos que a segunda é condição
necessária para a primeira, então temos que mudar a ordem delas e
aplicar o conectivo →(condicional):
Se
andré sai de casa, renato vai ao trabalho.
A próxima
informação traz que
Renato ir ao
trabalho é condição suficiente para Natália ir ao cinema
Aplicando a regra da
condição suficiente:
Se
renato vai ao trabalho, então Natália vai ao cinema.
Temos também as informações
de que
Marcos
encontrar Camila é condição necessária e suficiente para José
ficar alegre e é condição necessária para Natália ir ao cinema.
Aplicando
as regras da bicondicional e da condicional:
Marcos
encontra Camila se, e somente se, José fica alegre.
Se
Natália vai ao Cinema, então marcos encontra Camila.
Então,
unindo todas as informações temos:
p1:
Se andré sai de casa, renato vai ao trabalho.
P2:
Se renato vai ao trabalho, então Natália vai ao cinema.
P3:
Marcos encontra Camila se, e somente se, José fica alegre.
P4:
Se Natália vai ao Cinema, então marcos encontra Camila.
P5:
José não ficou alegre.
Agora
vamos descobrir o valor de cada uma das proposições simples que
formam essas proposições compostas. Para facilitar o entendimento
vamos pintar de verde as proposições verdadeiras e de vermelho as
falsas. Precisamos considerar todas as informações fornecidas pelo
enunciado como verdadeiras. O único valor que temos certeza, é a da
proposição P5, pois é uma proposição simples:
José
não ficou alegre.
Assim, sabemos que o
valor da sua negação será falso, então aplicando o valor na P3:
P3:
Marcos encontra Camila se, e somente se, José
fica alegre.
Em uma
bicondicional, se uma proposição é falsa, a outra também precisa
ser falsa, então:
P3:
Marcos encontra Camila se, e
somente se, José fica alegre.
Agora aplicaremos o
valor F dentro da proposição P4:
P4:
Se Natália vai ao Cinema, então marcos
encontra Camila.
Em uma condicional,
se a segunda proposição é falsa, com certeza a primeira também
será falsa.
P4:
Se Natália vai ao Cinema,
então marcos encontra Camila.
Agora aplicaremos o valor F dentro da proposição P2:
P2:
Se renato vai ao trabalho, então Natália
vai ao cinema.
Em uma
condicional, se a segunda proposição é falsa, com certeza a
primeira também será falsa.
P2:
Se renato vai ao trabalho,
então Natália vai ao cinema.
Agora aplicaremos o
valor F dentro da proposição P1:
p1:
Se andré sai de casa, renato vai
ao trabalho.
Em uma condicional,
se a segunda proposição é falsa, com certeza a primeira também
será falsa.
p1:
Se andré sai de casa,
renato vai ao trabalho.
Compilando todas as
informações:
p1:
Se andré sai de casa,
renato vai ao trabalho.
P2:
Se
renato vai ao trabalho, então Natália vai ao cinema.
P3:
Marcos encontra Camila se, e
somente se, José fica alegre.
P4:
Se Natália vai ao Cinema,
então marcos encontra Camila.
P5:
José não ficou alegre.
Concluímos então
que:
André não saiu de
casa
Renato não foi ao
trabalho
Natália não foi ao
cinema
Marcos não
encontrou Camila
José não ficou
alegre.
Analisando as
alternativas, percebemos que a única que está de acordo com nossos
conclusões é a letra a:
a) Renato não foi
ao trabalho e Marcos não encontrou Camila.
terça-feira, 17 de abril de 2018
Questão de geometria plana
Mais uma questão de geometria plana do Clube de Questões saindo do forno galera! Confiram:
Seja ABC um triângulo isóceles de base BC = (x+3) cm, com AB = (x+4) cm e AC = (3x-10)cm. A base de ABC mede _____cm.
a) 4
b) 6
c) 8
d) 10
Resolução no link:
Seja ABC um triângulo isóceles de base BC = (x+3) cm, com AB = (x+4) cm e AC = (3x-10)cm. A base de ABC mede _____cm.
a) 4
b) 6
c) 8
d) 10
Resolução no link:
sexta-feira, 13 de abril de 2018
Questão de Conversões de medidas e Geometria espacial
E aí galera, prontos para mais uma questão de RLM? Então vamos lá:
Uma caixa d’água,
na forma de um paralelepípedo retângulo cujas medidas são 0,120
dam de comprimento, 90 cm de largura e 1,35 m de altura, está com um
terço da respectiva capacidade com água. O volume d’água, em
metros cúbicos, que falta para deixar o reservatório completamente
cheio é de
a) 1,458.
b) 0,972.
c) 0,486.
d) 2,187.
e) 0,786.
Questão bem
interessante sobre conversões de medidas e geometria espacial.
Primeiramente, vamos converter todas as medidas para centímetros
para facilitar, lembrando que:
1 decâmetro (dam) =
1000 centímetros
1 metro = 100
centímetros
Para converter de
dam para cm, precisamos multiplicar por 1000:
0,120 x 1000 = 120
cm
Para converter de m
para cm, precisamos multiplicar por 100:
1,35 x 100 = 135 cm.
Pronto, agora que
temos todas as medidas em cm, fica mais fácil calcular o volume do
paralelepípedo retângulo, cujo resultado é obtido pela fórmula:
V=Abase x
altura
A área da base será
o produto dos comprimentos dos lados do retângulo que formam a base:
Abase=
120x90
Abase=
10800
Substituindo na
fórmula do volume
V=Abase x
altura
V = 10800 x 135
V = 1458000 cm3
Se o recipiente está
com 1/3 de seu volume coberto com água, então faltam 2/3 para
completá-lo, ou seja:
2/3 x 1458000
=972000 cm3
Como as respostas
estão em m3, precisamos converter, para converter de cm3
para m3, precisamos dividir por 1003, ou seja,
por 1000000:
972000/1000000=0,972
Gabarito então,
letra b.
quinta-feira, 12 de abril de 2018
Questão de Tabela Verdade (Cespe - 2018)
E aí fãs do raciocínio lógico, bora resolver mais uma questão???
E aí, já sabe a resposta? então confira a resolução no link https://youtu.be/z3BZfKyliHA
segunda-feira, 9 de abril de 2018
Questão de proposições lógicas compostas
Fala galera, bora começar a semana com uma questão de proposições lógicas?
Imagine que você possa ganhar um de três prêmios diferentes (X, Y e Z). O prêmio mais valioso é X e o segundo mais valioso é Y. Para ganhar um dos prêmios, você deve proferir uma sentença que seja verdadeira. Se a sentença for falsa, você não ganha nenhum dos prêmios. Qual das sentenças nas alternativas a seguir, se proferida, garante que você ganha o prêmio mais valioso?
a) Eu ganharei o prêmio Y, e não o prêmio Z.
b) Eu ganharei nem o prêmio X e nem o prêmio Y.
c) Eu ganharei o prêmio Z, e não o prêmio Y.
d) Eu ganharei nem o prêmio Y e nem o prêmio Z.
e) Eu ganharei o prêmio Y ou o prêmio Z.
E aí, já sabe a resposta?
Confira a resolução e o gabarito no canal do Clube de Questões
https://www.youtube.com/watch?v=-3rf6QRPrFM
sábado, 7 de abril de 2018
Inequações de segundo grau
E aí galera! Preparados para uma questão sinistra de inequações de 2o grau?? então vamos que vamos!!

Já sabe resolvê-la?? Se não, confira abaixo a resolução:
Temos aqui uma questão bem complexa e interessante de inequações de 2o grau. Temos a inequação x² - 75x + 1400 < 0, e precisamos descobrir todos os valores inteiros que satisfazem essa desigualdade, ou seja, todos os valores de x que resultarão em f(x) menor do que 0.
Vamos primeiramente analisar nossa função quadrática.
Coeficientes:
a = 1
b = -75
c = 1400
Como o coeficiente a é positivo, no gráfico teremos uma parábola com concavidade voltada para cima.
Resolvendo pela fórmula de bháskara ou por soma e produto, temos que as raízes da equação serão:
x`= 35
x``= 40
Ou seja, o gráfico tocará o eixo x quando x for igual a 35 e 40. Por ser uma parábola com a concavidade voltada para cima, f(x) será positiva quando: 40<= x <= 35, ou seja, quando x for maior ou igual a 40, ou x for menor ou igual a 35.
Porém nós precisamos descobrir quando f(x) será negativa, que consequentemente será quando: 35 < x < 40, ou seja, x for um número entre 35 e 40.
Vamos visualizar no gráfico para facilitar:

Repare que a parte em que f(x) é negativa, é apenas quando x está entre 35 e 40.
A questão ainda informa que x precisa ser um número inteiro, então vamos listar os números inteiros que estão entre 35 e 40:
36, 37, 38 e 39.
A soma desses valores será a quantidade em centilitros:
36+37+38+39 = 150 centilitros.
Porém a questão traz as alternativas em cm ³, então vamos primeiramente converter para mililitros, sendo que 1 centilitro equivale a 10 mililitros, então:
150 x 10 =1500 mililitros
Sabemos também que 1 mililitro equivale a 1 cm³, portanto, o gabarito é a letra a .
quarta-feira, 4 de abril de 2018
Questão de negação de proposições na nova série Questão Smart!
Fala Galera! Já conferiram a nova série do Smart Study? É a Questão Smart!
Nessa série, resolveremos questões de concursos e vestibulares sugeridas por vocês!
Confira a primeira questão da série e clique no link para ver a resolução:
https://youtu.be/R1m3ybsE1pM
Envie a questão que você gostaria de ver resolvida para o e-mail estudiosmartstudy@gmail.com com o assunto: "Questão Smart"
Se a sua questão for escolhida, publicaremos a resolução!
Nessa série, resolveremos questões de concursos e vestibulares sugeridas por vocês!
Confira a primeira questão da série e clique no link para ver a resolução:
https://youtu.be/R1m3ybsE1pM
Envie a questão que você gostaria de ver resolvida para o e-mail estudiosmartstudy@gmail.com com o assunto: "Questão Smart"
Se a sua questão for escolhida, publicaremos a resolução!
sexta-feira, 30 de março de 2018
Questão de equivalências lógicas
Fala galera! Vamos começar o feriado com uma questão de proposições equivalentes? haha
Banca: FCC
Órgão: ALSP - Assembléia
Legislativa do Estado de São Paulo
Cargo: Administrador de Banco de
Dados
E aí, descobriu a resposta? Se não descobriu, clique no link para ver a resolução!
quarta-feira, 28 de março de 2018
Bem vindos ao Blog do Prof. Roger Saruhashi
Olá pessoal!
Bem vindos ao Blog do Professor Roger Saruhashi.
Neste blog traremos materiais muito interessantes de Matemática e Raciocínio Lógico para facilitar seus estudos.
Trabalharemos com conteúdos tanto para concursos públicos quanto para vestibulares e Enem.
E já vamos inaugurar o blog com uma questão comentada de raciocínio lógico:

Questão que parece difícil mas é preciso simplesmente interpretá-la com calma.
Vamos chamar de x o número de filhos de Pedro.
Agora vamos montar a equação por partes:
Triplo do quadrado de filhos = 3.x²
63 menos 12 vezes o número de filhos = 63 - 12.x
Juntando as informações temos que
3.x² = 63 -12.x
Organizando melhor essa equação chegamos a uma equação de 2o grau que pode ser resolvida por BHASKARA ou soma e produto:
3.x² + 12.x - 63 = 0
Então,
A = 3
B = 12
C = -63
Pelo método da soma e produto:
X' + X" = -B/A
X' + X" = -12/3=4
X' + X" =4
X'.X" = c/a
X'.X" = -63/3
X'.X" =-21
Ou seja, precisamos descobrir quais números que somados resultam em =4 e multiplicados são -21.
Estes números são:
X' = 3
X" = -7
Como o número de filhos não pode ser negativo, a resposta é 3, gabarito letra C.
Bem vindos ao Blog do Professor Roger Saruhashi.
Neste blog traremos materiais muito interessantes de Matemática e Raciocínio Lógico para facilitar seus estudos.
Trabalharemos com conteúdos tanto para concursos públicos quanto para vestibulares e Enem.
E já vamos inaugurar o blog com uma questão comentada de raciocínio lógico:

Questão que parece difícil mas é preciso simplesmente interpretá-la com calma.
Vamos chamar de x o número de filhos de Pedro.
Agora vamos montar a equação por partes:
Triplo do quadrado de filhos = 3.x²
63 menos 12 vezes o número de filhos = 63 - 12.x
Juntando as informações temos que
3.x² = 63 -12.x
Organizando melhor essa equação chegamos a uma equação de 2o grau que pode ser resolvida por BHASKARA ou soma e produto:
3.x² + 12.x - 63 = 0
Então,
A = 3
B = 12
C = -63
Pelo método da soma e produto:
X' + X" = -B/A
X' + X" = -12/3=4
X' + X" =4
X'.X" = c/a
X'.X" = -63/3
X'.X" =-21
Ou seja, precisamos descobrir quais números que somados resultam em =4 e multiplicados são -21.
Estes números são:
X' = 3
X" = -7
Como o número de filhos não pode ser negativo, a resposta é 3, gabarito letra C.
Assinar:
Comentários (Atom)
Questão de argumentação lógica
Questão Cespe dificílima saindo do forno no Questão Smart! Questão do dia: De uma urna que continha 20 bolas idênticas, identificadas p...
-
Bom dia galera! Um assunto pouco compreendido de RLM é o de condições necessárias e suficientes, por isso trouxe uma questão com a resolução...
-
Mais uma questão resolvida no Clube de Questões - Questões de Concursos Públicos Questão do dia Para executar a tarefa de manutenção de 111 ...




